2018—2019学年第一学期期末考试
九年级数学试题参考答案及评分标准
说明:
1.阅卷过程中,如学生还有其它正确解法,可参照评分标准按步骤酌情给分.
2.坚持每题评阅到底的原则,当学生的解答在某一步出现错误,影响了后继部分时,如果该步以后的解答未改变这一题的内容和难度,可视影响的程度决定后面部分的给分,但不得超过后继部分应给分数的一半;如果这一步后面的解答有较严重的错误,就不给分.
3.解答右端所注分数,表示正确做到这一步应得的累加分数.只给整数分数.
一、选择题(本大题共16个小题,1—10小题,每小题3分;11—16小题,每小题2分,共42分。在每小题给出的四个选项中,只有一项是符合题目要求的)
|
题号 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
|
答案 |
B |
D |
D |
C |
A |
A |
C |
D |
D |
A |
B |
C |
B |
B |
C |
B |
二、填空题(本大题有3个小题,共12分.17~18小题各3分;19小题有2个空,每空3分.把答案写在题中横线上)
17.1 18.2029 19.![]() a
a ![]() a
a
三、解答题(本大题有7小题,共66分.解答应写出文字说明、证明过程或演算步骤)
20. (本题满分8分)
解:设正方形的边长为x厘米,那么矩形的长为(x+5)厘米,宽为(x+3)厘米,依题意有
(x+5)(x+3)=35, -----------------------------------------------------------------------------------5分
解得x1=2,x2=﹣10(负值舍去).------------------------------------------------------------------7分
答:正方形的边长为2厘米.-----------------------------------------------------------------------8分
21.(本题满分9分)
解:解:(1)∵PQ∥x轴,
∴点P的纵坐标为2,把y=2代入y=![]() 得x=3,
得x=3,
∴P点坐标为(3,2);---------------------------------------------------------------------4分
(2)∵S△POQ=S△OMQ+S△OMP,
∴![]() |k|+
|k|+![]() ×|6|=10,
×|6|=10,
∴|k|=14,而k<0,
∴k=﹣14. --------------------------------------------------------------------------------------9分
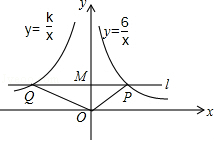
(第21题图)
22.(本题满分9分)
解:(1)如图所示,线段A1B1即为所求; ------------------------------------------------3分
(2)如图所示,线段A2B1即为所求;-------------------------------------------------------6分
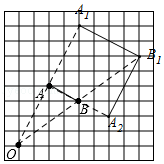
(第22题图)
(3)由图可得,四边形AA1B1A2为正方形,
∴四边形AA1B1A2的面积是(![]() )2=(
)2=(![]() )2=20.-----------------------9分
)2=20.-----------------------9分
23.(本题满分9分)
解:解:(1)答案不唯一,
例如“圆心角相等”、“半径和弧长对应成比例” ------------------------------------------3分
(2)m=![]() , ∴n=
, ∴n=![]() , 弧长=
, 弧长=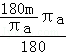 =2m. --------------------6分
=2m. --------------------6分
(3)∵两个扇形相似, ∴新扇形的圆心角为120°
设新扇形的半径为r,
则(![]() )2=
)2=![]() ⇒r=15
⇒r=15![]() .
.
即新扇形的半径为![]() cm. -------------------------------------------------------------9分
cm. -------------------------------------------------------------9分
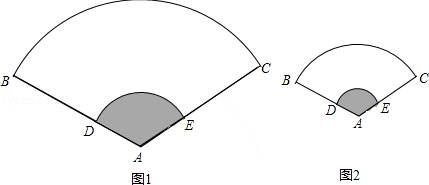
(第23题图)
24.(本题满分10分)
解:(1)∵转盘被等分成五个扇形区域,每个区域上分别写有“可”、“绿”、“乐”、“茶”、“红”字样;
∴一次“有效随机转动”可获得“乐”字的概率为:![]() ; ---------------------------------------5分
; ---------------------------------------5分
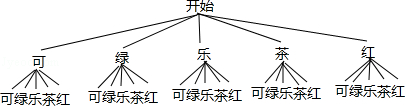
(2)画树状图得
∵共有25种等可能的结果,其中该顾客经过两次“有效随机转动”后,获得奖品有6种情况,
∴该顾客经过两次“有效随机转动”后,获得奖品的概率为![]() . ----------------------10分
. ----------------------10分
(第24题图)
25. (本题满分10分)
解:(1)∵CD是⊙O的切线,
∴OC⊥CD,
∵AD⊥CD,
∴AD∥OC,
∴∠DAC=∠OCA,
∵OC=OA,
∴∠OCA=∠OAC,
∴∠OAC=∠DAC,
∴AC平分∠DAO; -------------------------------------------------------------------------5分
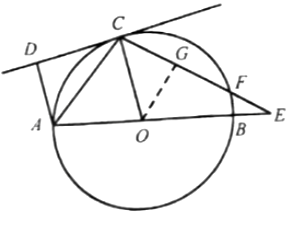
(2)①∵AD∥OC,
∴∠EOC=∠DAO=105°,
∵∠E=30°,
∴∠OCE=45°;
②作OG⊥CE于点G,
则CG=FG=OG,
∵OC=![]() ,∠OCE=45°,
,∠OCE=45°,
∴
(第25题图)
CG=OG=1,
∴FG=1,
在Rt△OGE中,∠E=30°,
∴GE=![]() ,
,
∴EF=GE-FG=![]() -1 ------------------------------------------------10分
-1 ------------------------------------------------10分
26. (本题满分11分)
解:(1)∵抛物线y=ax2+![]() x+4的对称轴是直线x=3,
x+4的对称轴是直线x=3,
∴﹣![]() =3,解得:a=﹣
=3,解得:a=﹣![]() ,
,
∴抛物线的解析式为y=﹣![]() x2+
x2+![]() x+4.
x+4.
当y=0时,﹣![]() x2+
x2+![]() x+4=0,
x+4=0,
解得:x1=﹣2,x2=8,
∴点A的坐标为(﹣2,0),点B的坐标为(8,0). ------------------------------------4分
(2)∵点M在抛物线上,所以点M的纵坐标是﹣![]() m2+
m2+![]() m+4
m+4
当x=0时,y=﹣![]() x2+
x2+![]() x+4=4,
x+4=4,
∴点C的坐标为(0,4).
设直线BC的解析式为y=kx+b(k≠0).
将B(8,0)、C(0,4)代入y=kx+b,
![]() ,解得:
,解得:![]() ,
,
∴直线BC的解析式为y=﹣![]() x+4.
x+4.
∵点N在直线BC上,且MN平行于Y轴,所以点N的坐标为(m,﹣![]() m+4)
m+4)
∵点M在第一象限
∴MN=﹣![]() m2+
m2+![]() m+4﹣(﹣
m+4﹣(﹣![]() m+4)=﹣
m+4)=﹣![]() m2+2m.
m2+2m.
又∵MN=3,
∴﹣![]() m2+2m=3.
m2+2m=3.
解得:m1=2,m2=6,
∴点M的坐标为(2,6)或(6,4); -------------------------------------------------------8分
(3)假设存在,设点P的坐标为(x,﹣![]() x2+
x2+![]() x+4),过点P作PD∥y轴,交直线BC于点D,则点D的坐标为(x,﹣
x+4),过点P作PD∥y轴,交直线BC于点D,则点D的坐标为(x,﹣![]() x+4),如图所示.
x+4),如图所示.
∴PD=﹣![]() x2+
x2+![]() x+4﹣(﹣
x+4﹣(﹣![]() x+4)=﹣
x+4)=﹣![]() x2+2x,
x2+2x,
∵S△PBC= S△PCD+ S△PBD
∴△PCD与△PBD可以看做成以PD为底,两高之和为OB的三角形
∴S△PBC=![]() PD•OB=
PD•OB=![]() ×8•(﹣
×8•(﹣![]() x2+2x)=﹣x2+8x=﹣(x﹣4)2+16.
x2+2x)=﹣x2+8x=﹣(x﹣4)2+16.
∵﹣1<0,
∴当x=4时,△PBC的面积最大,最大面积是16. --------------------------------------11分
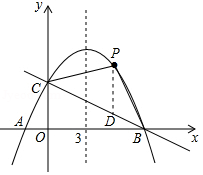
(第26题图)
19.解:(1)∵AD1=![]() AB,AE1=
AB,AE1=![]() AC,∠A=∠A,
AC,∠A=∠A,
∴△AD1E1∽△ABC,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
∴D1E1=![]() =
=![]() a;
a;
故答案为:![]() a;
a;
(2)∵AD1=![]() AB,AE1=
AB,AE1=![]() AC,D1D2=
AC,D1D2=![]() D1B,E1E2=
D1B,E1E2=![]() E1C,∠A=∠A,
E1C,∠A=∠A,
∴△AD2E2∽△ABC,
∵D1D2=![]() D1B,
D1B,
∴AD2=AD1+D1D2=![]() AB+
AB+![]() (AB﹣
(AB﹣![]() AB)=
AB)=![]() AB,
AB,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,解得D2E2=
,解得D2E2=![]() a=
a=![]() a,
a,
故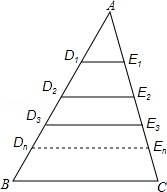 答案为:
答案为:![]() a;
a;
(3)∵同(1)可得△AD3E3∽△ABC,
∴D3E3=![]() a=
a=![]() a,
a,
故答案为:![]() a;
a;
(第19题图)
(4)由(1)(2)(3)可知,DnEn=![]() a,
a,
故答案为:![]() a.
a.
2018-2019学年第一学期期末九年级数学答案 第
